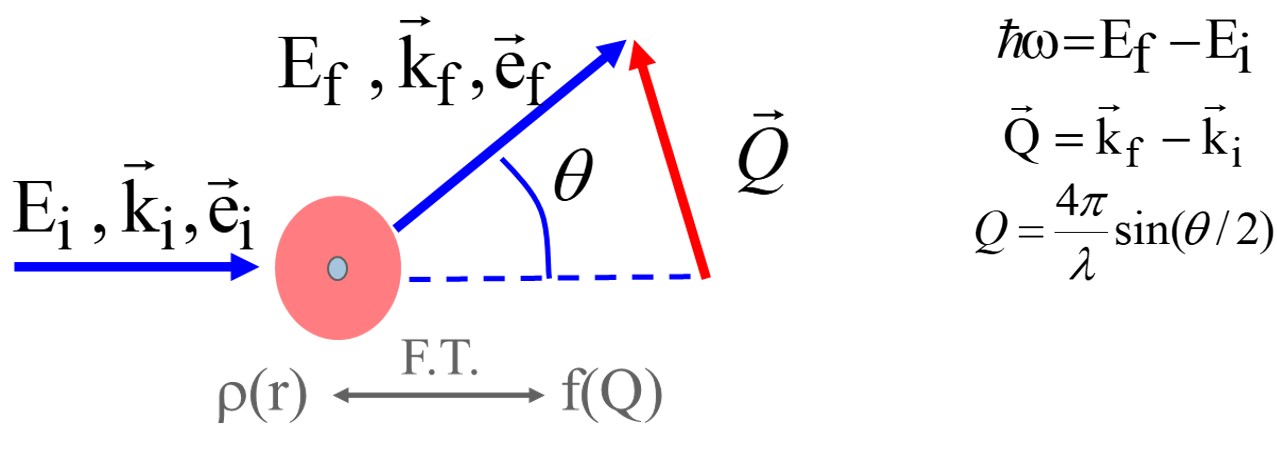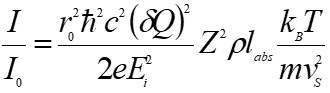| Introduction |
Momentum-resolved inelastic x-ray scattering (IXS) technique with few-milli electron volt (meV) energy resolution has become a powerful tool in real materials of fundamental and technological importance, spanning a broad spectrum of scientific disciplines from fundamental physics and materials science to biophysics and geophysics. Momentum-resolved IXS has been successfully employed to study collective excitations as a function of energy and momentum transfer for single crystals, polycrystalline samples, disordered systems and liquids by measuring dynamical structure factor S(Q,w), which is the space and time Fourier transform of the density-density correlation function. The technique is non-destructive and probes the bulk properties of a given structure. It is very suitable for a wide range of parameters, e.g., temperature, pressure, and chemical doping. |
| Comparison to Other Techniques |
In principle, momentum-resolved IXS technique is complementary to inelastic neutron scattering (INS) for studying dynamical properties of materials on mesoscopic-length scales. The main advantages compared to INS are:
In contrast to Raman and Brillouin spectroscopies, which are limited to:
Detailed discussions for instrumentation and science cases can be found in following review papers:
|
| Scattering Process for X-rays |
A general scattering process can be shown as in the following figure and valid for probes like neutrons, photons and electrons. Incident photon of initial energy of well-defined Ei, momentum ki , and polarization ei impinges on a target. Target is an atom which consists of nucleus and electrons. Then, incident beam is scattered by these electrons to different state (by Ef, kf, ef) and we can observe the scattered intensity at certain scattering angle theta in a certain solid-angle element dW.
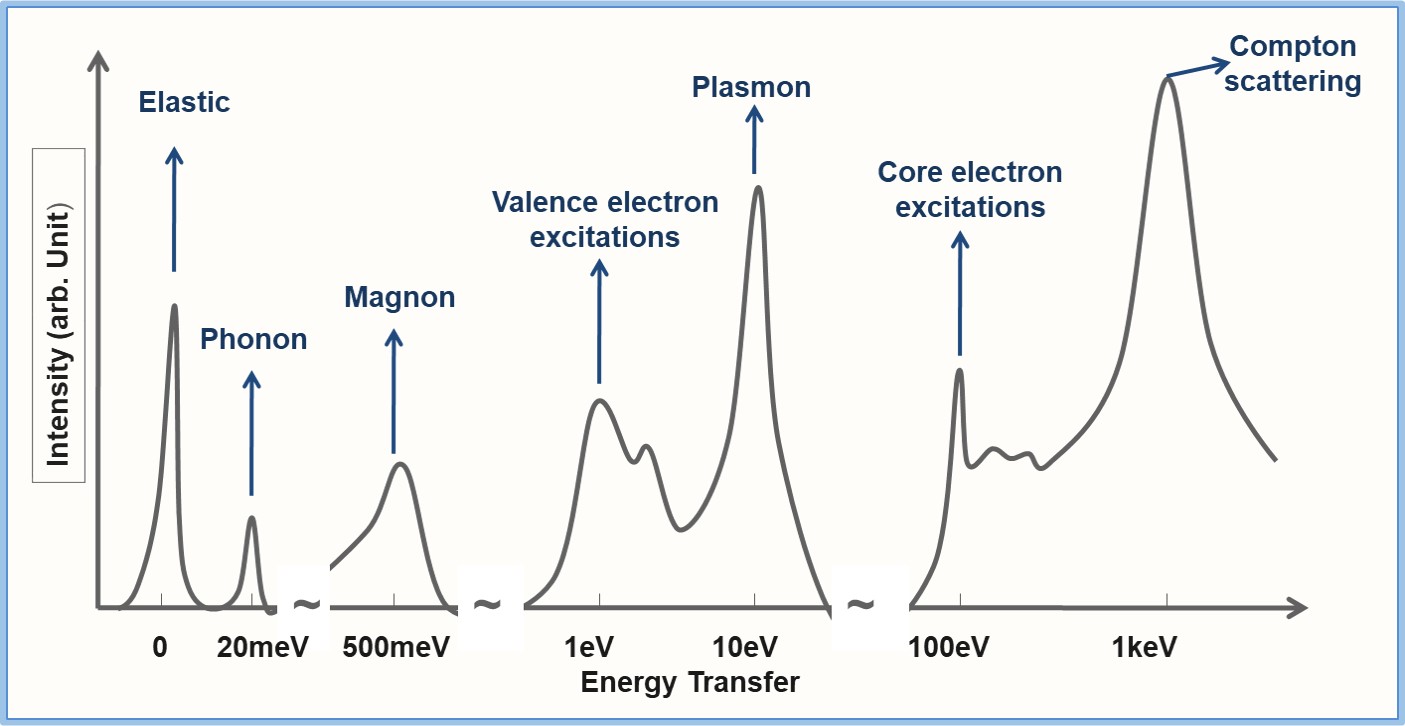
The spectrum, S(Q,w), as a function of energy and momentum transfer gives direct information on excitations specific to the studied system.
|
| Partial Differential Cross Section |
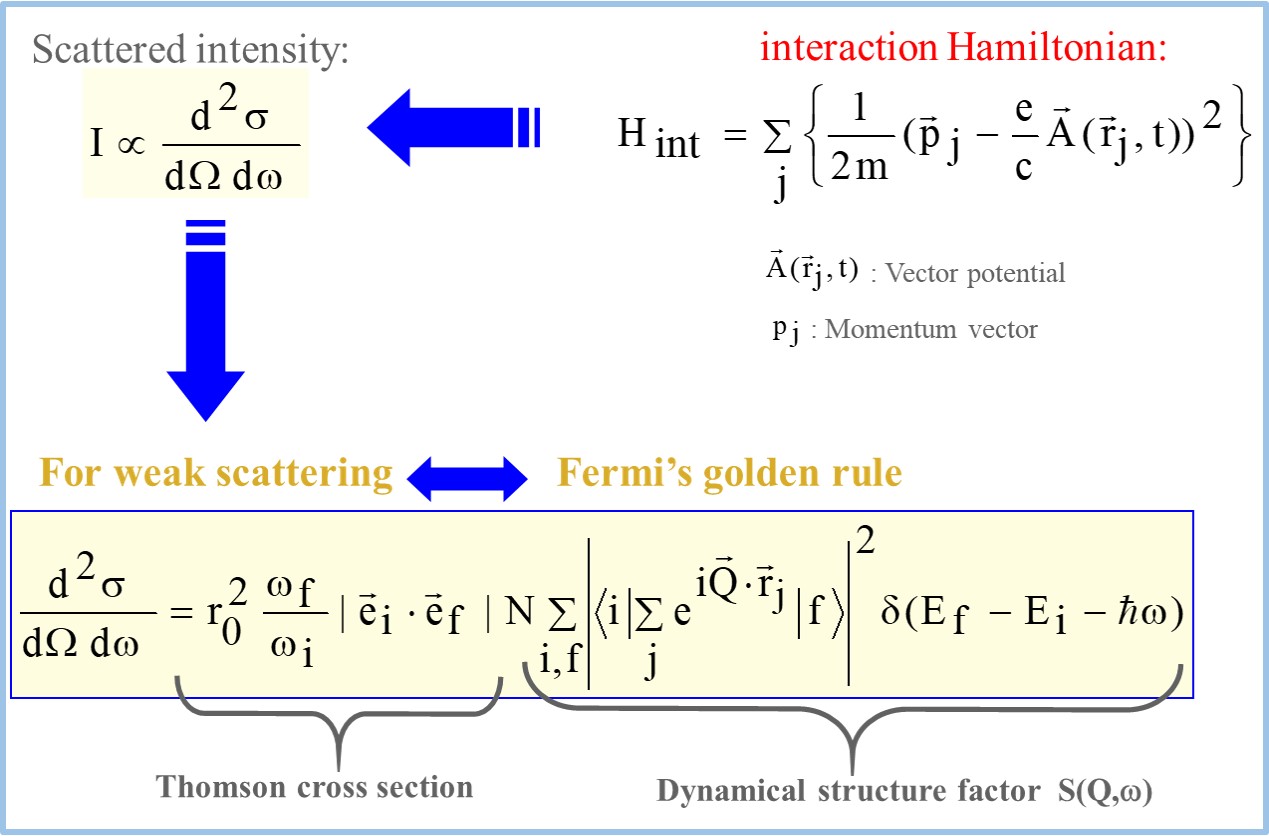
The scattered intensity is described by the partial differential cross section which can be calculated by considering the interaction Hamiltonian of the scattering system.
For weak scattering process, it can be written in terms of the Fermi’s Golden rule.
J. J. Sakurai, Advanced Quantum Mechanics, Addison-Wesley Publishing Company, New York, pg. 20-57,1967. |
| Dynamical Structure Factor |
Dynamical structure factor can also be represented as time Fourier transform of the density-density correlations function at different times for the same initial and final states by using van-Hove transformation. Within the adiabatic approximation, it can be expressed as density-density correlation at different times for the same nuclei state. And f is the atomic form factor that depends on the electron wave function.
At the end, dynamical structure factor for one phonon case can be written as follows:
|
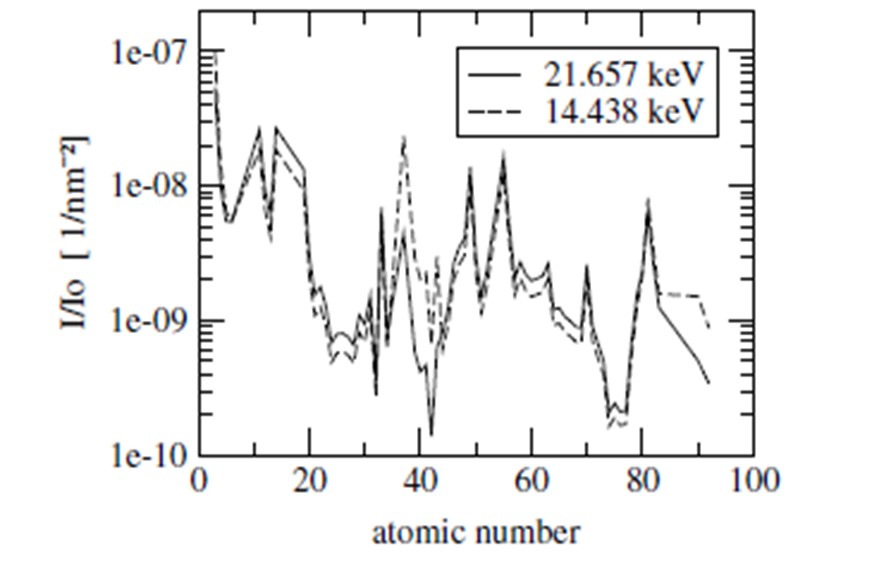
| Expected Phonon Intensities (Phonon Cross Section) |
The scattered intensity is described by the partial differential cross section which can be calculated by considering the interaction Hamiltonian of the scattering system.
where dQ is the momentum resolution, Ei is the incident energy, Z is the number of electrons, Iabs is the absorption length chosen for the optimum thickness, r is the number and ns is the sound velocity.
Expected phonon intensities for different elements in forward scattering, normalized to the incident flux on the sample and 1 nm−2 momentum resolution for two incident energies at 14.4 and 21.6 keV. As seen in this figure, phonon cross section is too low and presents a real challenge for inelastic x-ray scattering .
H. Sinn, Spectroscopy with meV energy resolution, J. Phys.: Condens. Matter,13, 7525, 2001 |